LP3233 [HNOI2014]世界树 [虚树/树上乱搞]
据说做完这题虚树就入门了...
这根本不是树状 dp...qwq
Problem
世界树是一棵无比巨大的树,它伸出的枝干构成了整个世界。在这里,生存着各种各样的种族和生灵,他们共同信奉着绝对公正公平的女神艾莉森,在他们的信条里,公平是使世界树能够生生不息、持续运转的根本基石。
世界树的形态可以用一个数学模型来描述:世界树中有 n 个种族,种族的编号分别从 1 到 n,分别生活在编号为 1 到 n 的聚居地上,种族的编号与其聚居地的编号相同。有的聚居地之间有双向的道路相连,道路的长度为 1。保证连接的方式会形成一棵树结构,即所有的聚居地之间可以互相到达,并且不会出现环。定义两个聚居地之间的距离为连接他们的道路的长度;例如,若聚居地 a 和 b 之间有道路,b 和 c 之间有道路,因为每条道路长度为 1 而且又不可能出现环,所卧 a 与 c 之间的距离为 2。
出于对公平的考虑,第 i 年,世界树的国王需要授权 m[i]个种族的聚居地为临时议事处。对于某个种族 x(x 为种族的编号),如果距离该种族最近的临时议事处为 y(y 为议事处所在聚居地的编号),则种族 x 将接受 y 议事处的管辖(如果有多个临时议事处到该聚居地的距离一样,则 y 为其中编号最小的临时议事处)。
现在国王想知道,在 q 年的时间里,每一年完成授权后,当年每个临时议事处将会管理多少个种族(议事处所在的聚居地也将接受该议事处管理)。 现在这个任务交给了以智慧著称的灵长类的你:程序猿。请帮国王完成这个任务吧。
Solution
从很明显的虚树性质来看
应该建虚树
然后我们在虚树上 dp?怎么 dp
没办法呀(摊手)
于是我们可以这么想
我们可以先预处理出虚树上的每个点是被哪个点控制的
然后我们就知道了虚树上边两端点的控制点是不是相同的
如果相同的话,原树上夹在这两个点中间的点都被这个控制点控制
如果不同的话,我们就要算一下他们链上的分界线,下边归下边的控制点管,上边归上边的控制点管。
但如果原树上夹的不止一条链?
像这样:
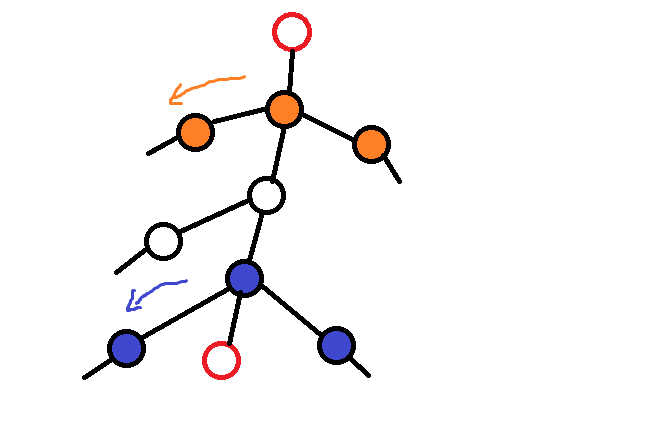
我们发现如果这两个点夹的链上的某个点
被这两个点之中的一个所管辖
那么这个点的所有子树都会被这个管辖
传递关系像这样:
于是按照这样的思路,我们只要算分界线就可以了
于是对距离和公式做一番分析
用倍增向上跳就 OK
因为这题的细节多,较复杂,因此不能面面俱到
剩下的细节请自行思考
Code
// Code by ajcxsu
// Problem: world_tree
#include<bits/stdc++.h>
using namespace std;
template<typename T> void gn(T &x) {
char ch=getchar();
x=0;
while(ch<'0' || ch>'9') ch=getchar();
while(ch>='0' && ch<='9') x=x*10+ch-'0', ch=getchar();
}
int n,u,v;
const int N=3e5+10, M=2e6+10;
int h[N], vt[N], to[M], nexp[M], p=1, bp;
inline void ins(int a, int b) { nexp[p]=h[a], h[a]=p, to[p]=b, p++; }
inline void vins(int a, int b) { nexp[p]=vt[a], vt[a]=p, to[p]=b, p++; }
const int OP=21;
int dfn[N], dep[N], siz[N], cnted[N], idx;
int gup[N][OP];
void dfs(int x, int k) {
dep[x]=k, dfn[x]=++idx, siz[x]=1;
for(int u=h[x];u;u=nexp[u])
if(!dfn[to[u]]) {
gup[to[u]][0]=x;
dfs(to[u], k+1);
siz[x]+=siz[to[u]];
}
}
void ini() {
dfs(1,1);
for(int j=1;j<OP;j++)
for(int i=1;i<=n;i++)
gup[i][j]=gup[gup[i][j-1]][j-1];
}
int lca(int s, int t) {
if(dep[s]<dep[t]) swap(s,t);
for(int j=OP-1;j>=0;j--)
if(dep[gup[s][j]]>=dep[t]) s=gup[s][j];
if(s!=t) {
for(int j=OP-1;j>=0;j--)
if(gup[s][j]!=gup[t][j]) s=gup[s][j], t=gup[t][j];
s=gup[s][0], t=gup[t][0];
}
return s;
}
int climb(int s, int k) {
if(k<0) return s;
for(int j=0;j<OP;j++) {
if(k&1) s=gup[s][j];
k>>=1;
}
return s;
}
int lis[N];
int id[N];
int ki;
bool que[N];
bool cmp(const int &a, const int &b) { return dfn[a]<dfn[b]; }
int stk[N], sz;
int rt;
int f[N];
typedef pair<int, int> mpair;
mpair bel[N];
void dp1(int x, int fa) {
bel[x].first=0x3f3f3f3f;
if(que[x]) bel[x].first=0, bel[x].second=x;
mpair com;
for(int u=vt[x];u;u=nexp[u]) {
dp1(to[u], x);
com=bel[to[u]], com.first+=dep[to[u]]-dep[x];
if(com<bel[x]) bel[x]=com;
}
f[bel[x].second]++;
} // 先从下往上更新管辖关系
void dp2(int x, int fa) {
if(fa && mpair(bel[fa].first+dep[x]-dep[fa], bel[fa].second)<bel[x]) {
f[bel[fa].second]++;
f[bel[x].second]--;
bel[x]=mpair(bel[fa].first+dep[x]-dep[fa], bel[fa].second);
} // 再从上往下更新管辖关系
int t, d=dep[x]-dep[fa], a=bel[fa].first, b=bel[x].first, up;
if(bel[x].second==bel[fa].second) {
t=climb(x, d-1);
f[bel[x].second]+=siz[t]-siz[x];
cnted[fa]+=siz[t];
}
else if(fa) {
up=(a+d-b)/2;
if((a+b-d)%2==0 && bel[fa].second<bel[x].second) up--;
t=climb(x, up);
f[bel[x].second]+=siz[t]-siz[x];
up=climb(x, d-1);
f[bel[fa].second]+=siz[up]-siz[t];
cnted[fa]+=siz[up];
}
else {
if(x!=1) f[bel[x].second]+=siz[1]-siz[x];
}
for(int u=vt[x];u;u=nexp[u])
dp2(to[u], x);
vt[x]=0;
}
int ans[N];
void solve() {
p=bp;
int rki=ki;
sort(lis, lis+ki, cmp);
sz=0;
stk[++sz]=0;
for(int i=0;i<rki;i++) {
int d=lca(stk[sz], lis[i]);
while(sz-1>0 && dep[stk[sz-1]]>=dep[d])
vins(stk[sz-1], stk[sz]), sz--;
if(stk[sz]!=d) vins(d, stk[sz]), stk[sz]=d, lis[ki++]=d;
stk[++sz]=lis[i];
}
rt=stk[2];
for(int i=2;i<sz;i++) vins(stk[i], stk[i+1]);
dp1(rt,0), dp2(rt,0);
for(int i=0;i<ki;i++) {
if(que[lis[i]]) {
ans[id[lis[i]]]+=f[lis[i]], f[lis[i]]=0;
}
int nfa=bel[lis[i]].second;
ans[id[nfa]]+=siz[lis[i]]-cnted[lis[i]]-1;
cnted[lis[i]]=0, bel[lis[i]]=bel[0], que[lis[i]]=0;
}
for(int i=0;i<rki;i++) {
printf("%d ", ans[i]);
ans[i]=0;
}
putchar('\n');
}
int main() {
gn(n);
for(int i=1;i<n;i++) gn(u), gn(v), ins(u,v), ins(v,u);
ini();
bp=p;
int q;
gn(q);
while(q--) {
gn(ki);
for(int i=0;i<ki;i++) gn(lis[i]), que[lis[i]]=true, id[lis[i]]=i;
solve();
}
return 0;
}