[HNOI2010] 矿场搭建
Problem
有不知道多少个矿场,某个矿场可能塌陷。问最少在哪些矿场建逃生通道可以使某个矿场塌陷后每个矿场的旷工都能安全离开。
Solution
当某个点被断开以后这个图会变成不连通——也就是割点。于是你可以找到所有被割点分开的联通块,以割点相连,于是这就变成了像是缩点以后的一棵树。找到度数为 1 的点,第一个答案就是度数为 1 的点个数,第二个答案就是度数的积。
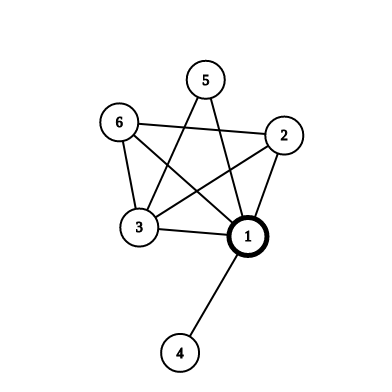
比如如下这图(样例 1),两个联通块:{3, 2, 5, 6} 和 {4},由 1 相连。
度数为 1 的联通块有两个。则需要在这两个联通块里面布置任意一个逃生通道就可以保证所有安全离开。因此总共的方案数为:4x1。
这个证明起来其实挺简单的。
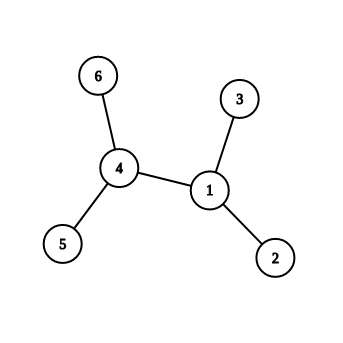
我们假设联通块最后缩成了这个样子(联通块之间的割点省略)。那么把 (6,4) 中间的割点给破坏掉,则我们可以发现,必须要在 6 中放置一个逃生通道,否则无法保证联通块 6 的安全。
因此我们首先得保证度数为 1 的联通块的安全。其次,度数不为一的点,破坏掉与它相连的任何一个割点,那么它总可以从另一个割点到达度数为 1 的联通块。因此这样的策略是正确的。
但是还有一个问题。假如没有割点。那么如果你只在这个联通块里放置一个逃生通道,是绝对有问题的。因为如果塌的是这个逃生通道,所有人都不能逃走。因此得至少放置两个逃生通道,而这两个逃生通道的位置是可以随便选的。因此若点数为 $n$,特判方案数为 $\frac {n(n-1)}{2}$。
Code
// Code by ajcxsu
// Problem: Mine
#include<bits/stdc++.h>
#define CLR(x) memset(x,0,sizeof(x))
using namespace std;
const int N=1e3,M=2e3;
int h[N],to[M],nexp[M],p=1;
inline void ins(int a,int b) { nexp[p]=h[a], h[a]=p, to[p]=b, p++; }
/* tarjan */
int dfn[N],low[N],idx,root;
int cut[N],col[N];
void tarjan(int x, int f) {
dfn[x]=low[x]=++idx;
int cnt=0;
for(int u=h[x];u;u=nexp[u])
if(!dfn[to[u]]) {
cnt++;
tarjan(to[u], x);
low[x]=min(low[x], low[to[u]]);
if(low[to[u]]>=dfn[x] && f!=-1 && !cut[x]) cut[x]=1;
}
else if(to[u]!=f) low[x]=min(low[x], dfn[to[u]]);
if(f==-1 && cnt>=2 && !cut[x]) cut[x]=1;
}
/* paint */
set<int> h2[N]; // 统计度数
int siz[N]; // 统计联通块大小
int cidx; // 统计联通块个数
void bfs(int s, int c) {
queue<int> qu;
qu.push(s);
col[s]=c;
while(!qu.empty()) {
int na=qu.front();
qu.pop();
siz[c]++;
for(int u=h[na];u;u=nexp[u])
if(!cut[to[u]] && !col[to[u]]) col[to[u]]=c, qu.push(to[u]);
else if(cut[to[u]]) h2[c].insert(to[u]);
}
}
inline void init() {
CLR(h), p=1, CLR(cut);
CLR(siz), CLR(col), CLR(dfn), CLR(low), idx=0;
for(int i=1;i<=cidx;i++) h2[i].clear();
cidx=0;
}
int main() {
ios::sync_with_stdio(false);
int n,T=0;
while(cin>>n, n) {
init();
int u,v;
int na=0;
for(int i=0;i<n;i++) cin>>u>>v, ins(u,v), ins(v,u), na=max(na,max(u,v));
n=na;
for(int i=1;i<=n;i++) if(!dfn[i]) root=i, tarjan(i, -1);
for(int i=1;i<=n;i++) {
if(!cut[i] && !col[i]) ++cidx, bfs(i, cidx);
}
long long ansa=0, ansb=1;
for(int i=1;i<=cidx;i++)
if(h2[i].size()<=1) ansa++, ansb*=siz[i];
++T;
if(ansa==1) ansa=2, ansb=ansb*(ansb-1)/2;
cout<<"Case "<<T<<": "<<ansa<<' '<<ansb<<endl;
}
return 0;
}