Problem

最小生成树

Solution

详见：http://www.yichenxing.com/2017/07/19/boruvkas-algorithm/ （地址已失效）

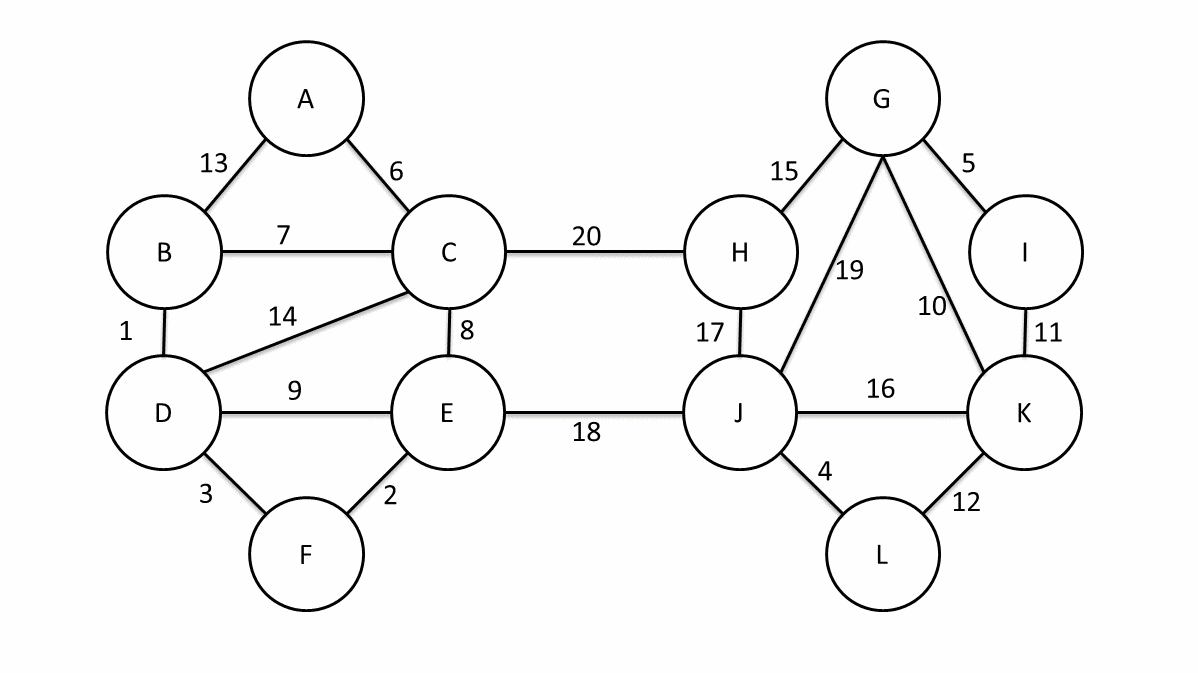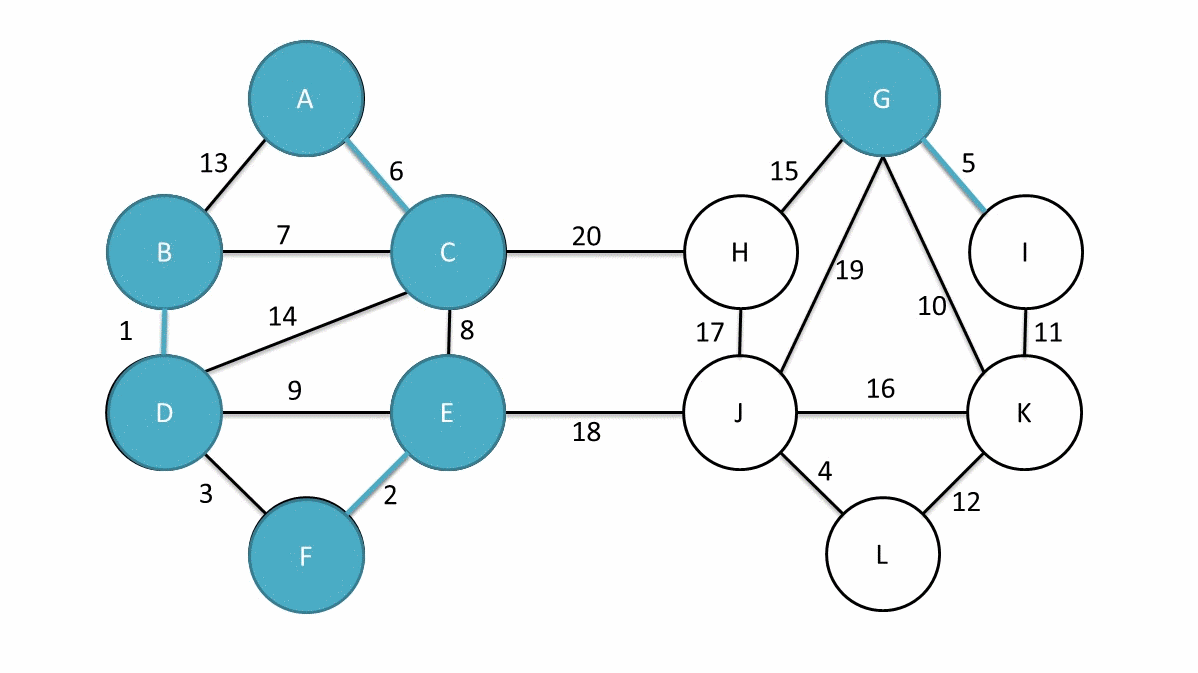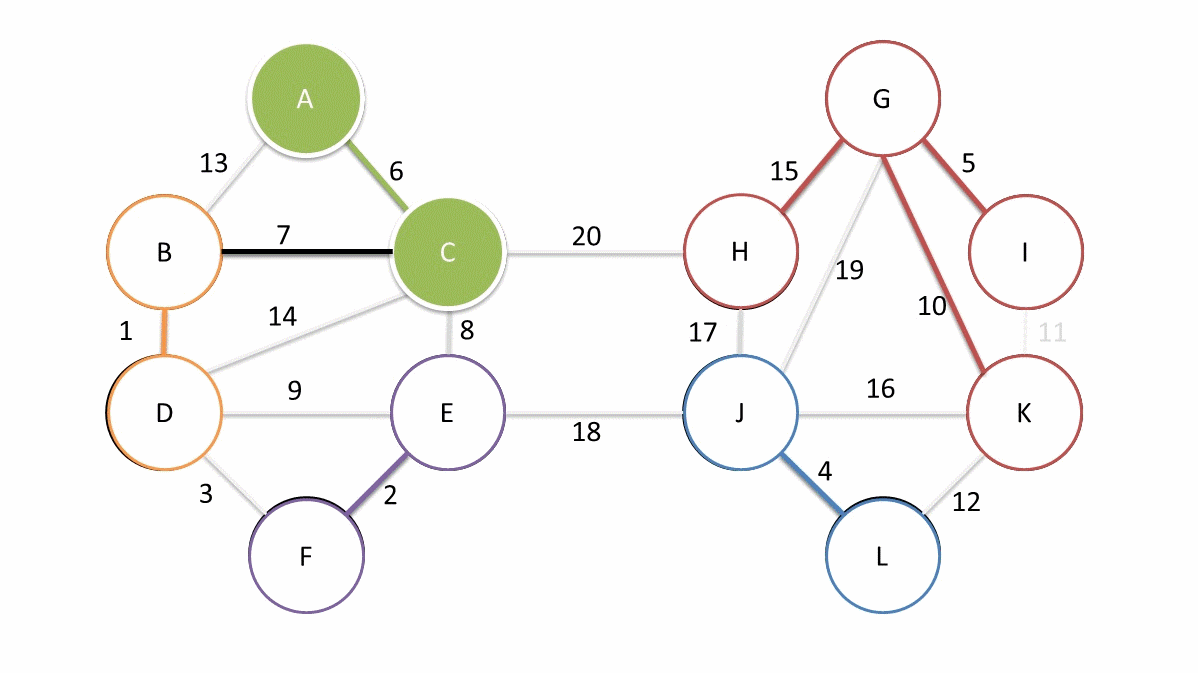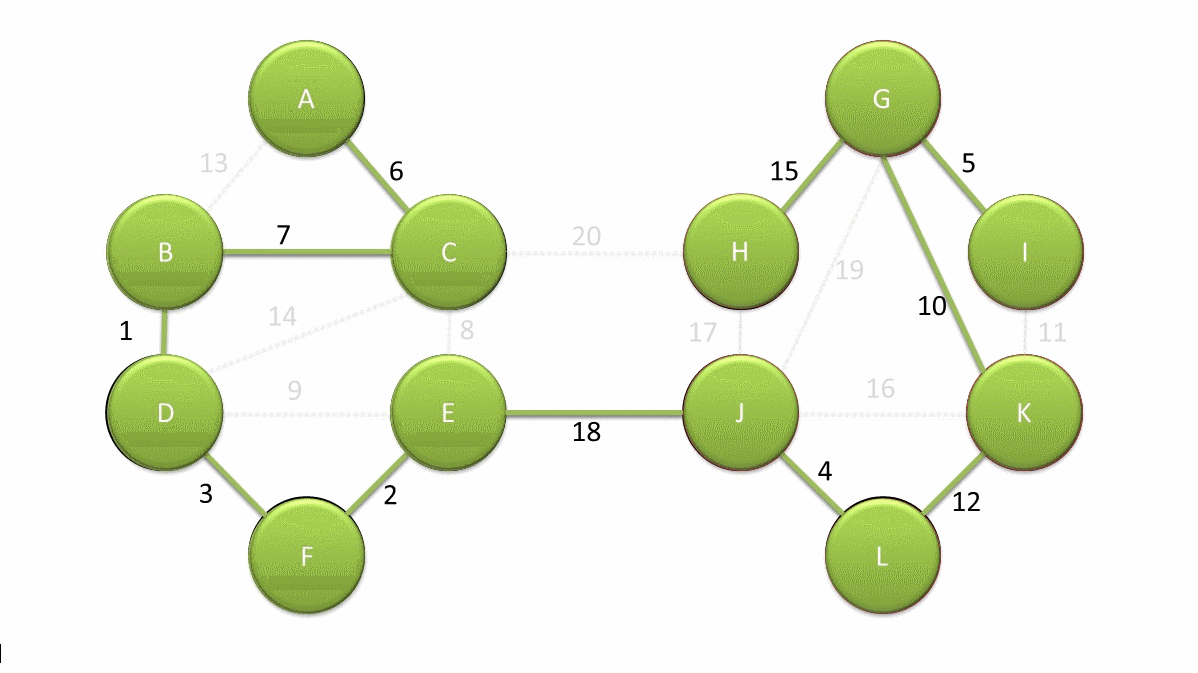
Boruvka 算法的演示如下（引自英文维基 en.wikipedia.org）：

复杂度：最坏 $O((n+m)logn)$，随机图 $O(n+m)$。

可能实现不怎么样....

Code

// Code by ajcxsu
// Problem: Boruvka

#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std;

const int N=5e3, M=2e5+10;
int u[M],v[M],w[M];
bool del[M];
int mst, ne[N]; // 最小生成树边权、集合邻近最小边权

int fa[N];
inline int Find(int x) {
    if(!fa[x]) return x;
    return fa[x]=Find(fa[x]);
}
inline void Union(int a,int b) { fa[Find(a)]=Find(b); }

inline void upd(int m,int x) { if(ne[x]==-1 || w[ne[x]]>w[m]) ne[x]=m; } // 更新最小边权
int main() {
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=0;i<m;i++) scanf("%d%d%d",&u[i],&v[i],&w[i]);
    int cnt=0;
    int af,bf;
    memset(ne,-1,sizeof(ne));
    while(cnt!=n-1) {
        for(int i=0;i<m;i++)
            if(!del[i]) {
                af=Find(u[i]), bf=Find(v[i]);
                if(af==bf) continue;
                upd(i, af), upd(i, bf);
            }
        bool sol=0;
        for(int i=1;i<=n;i++) {
            if(ne[i]!=-1 && !del[ne[i]]) {
                int x=ne[i];
                Union(u[x],v[x]), mst+=w[x], del[x]=1;
                sol=1;
                cnt++;
            }
            ne[i]=-1;
        }
        if(!sol) printf("orz\n"), exit(0);
    }
    printf("%d\n",mst);
    return 0;
}