乘船问题

$n$ 个人，重量为 $w_i$，一艘船载重上限为 $m$，每艘船最多载 2 人。
求装下 n 个人至少需要多少艘船。

Solution

让最轻的人和尽量重的人同坐一艘船。

不相交区间问题

数轴上有 $n$ 个开区间 $(a_i,b_i)$，选择尽量多两两不相交的区间。

Solution

排序成 $b_1\leq b_2 \leq ... \leq b_n$ 之后，一定选择第一个区间，再按顺序选择不相交区间。

证明

排序之后，有两种情况：

• $a_1\geq a_2$ 此时第一个区间一定被第二个区间包含，所以选择第一个区间更好。这种情况应当全部排除。
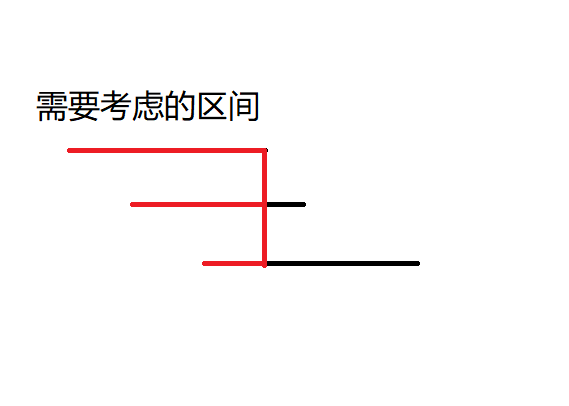
• $a_1< a_2$ 排除所有第一种情况之后，会变成这样：
  
  这样子交错的区间。
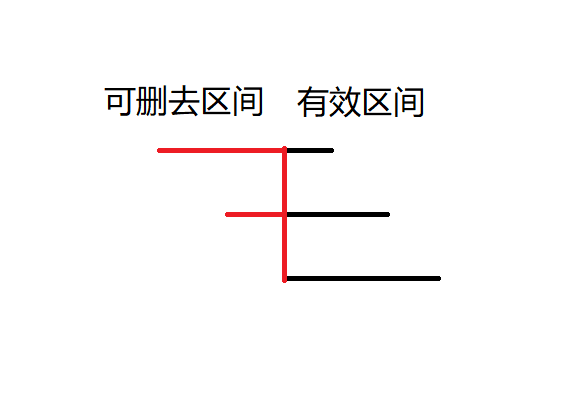
  我们现在是在区间 1 和区间 2 之间选择，所以对于区间 3（也代表了后面的区间），区间 1 和区间 2 的有效区间如图所示。那么这样的话，无效区间是可以删去的。
  发现区间 1 的有效区间被区间 2 所包含，因此按照贪心策略，选择第一个区间更好。

由归纳法可以证明，本贪心策略是正确的。

区间选点问题

数轴上有 $n$ 个闭区间 $[a_i,b_i]$，选择尽量少的点使每个区间至少包含一个点。

Solution

排序成 $b_1\leq b_2 \leq ... \leq b_n$ 之后，选择第一个区间的右端点，往右扫找到第一个不被第一个区间的右端点包含的区间，再选择这个区间的右端点，以此类推。

证明

与不相交区间类似。

• $a_1\geq a_2$ 此时无论在 1 区间选那个点都会被 2 区间包含，因此选区间 1 更优。
• $a_1< a_2$ 排除掉 1 情况后，为了包含区间一，可选择的方案：
  
  只能在如下的区间范围里考虑。
  为了使点覆盖尽量远的范围，选择区间 1 的右端点，显然。

归纳法可证明该贪心正确。

例题 UVa1615 Highway

可前往洛谷查看翻译题面。
将其显然地转化成区间选点问题处理。
注意是 欧几里得距离 。
注意 有多组数据。

// Code by ajcxsu
// Porblem: highway
#include<bits/stdc++.h>
#define eps (1e-15)
using namespace std;

typedef long long ll;

const int N=1e5+10;
struct Region { double l, r; } a[N];
bool cmp(const Region &a, const Region &b) {
    return a.r<b.r;
}

int main() {
    ios::sync_with_stdio(false);
    ll l,d,n;
    double x,y;
    while(cin>>l>>d>>n) {
        for(int i=0;i<n;i++) {
            cin>>x>>y;
            y=sqrt(d*d-y*y);
            a[i].l=max(x-y, 0.0), a[i].r=min(x+y, 1.0*l);
        }
        sort(a, a+n, cmp);
        double s=-1;
        int ans=0;
        for(int i=0;i<n;i++) {
            if(a[i].l-s>eps) s=a[i].r, ans++;
        }
        cout<<ans<<endl;
    }
    return 0;
}

区间覆盖问题

给定多个闭区间 $[a_i, b_i]$，选出最少的区间覆盖区间 $[s,t]$。

Solution

不是个很傻比的问题吗？
先把超出 s 和 t 的部分切了
然后选择左端点为 s，右端点尽量往右的区间。
然后 s 就会向右移动了
然后再回到第一步，循环直到 $s=t$ 就行啦？

证明：显然

Huffman 编码问题

就是合并果子啦