差分约束浅析
1 差分约束系统(system of difference constraints)
$n$ 个变量,$m$ 个不等式,形如 $x_i-x_j\leq a_k$ 或 $x_i-x_j\geq a_k$ 的不等式组称作差分约束系统
2 所要求的
$x_i-x_j$ 的最大 / 最小值。
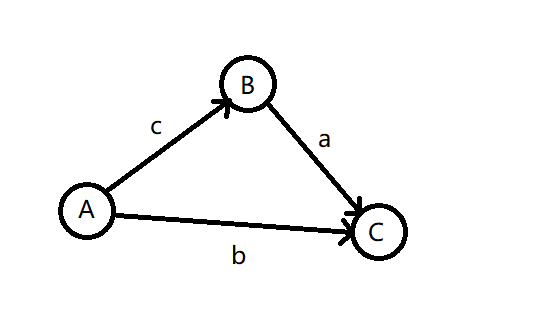
3 三角不等式
$$ \left\{\begin{matrix}B-A\leq c \\ C-B\leq a \\ C-A\leq b \end{matrix}\right. \Rightarrow C-A\leq a+c $$
$C-A$ 的最大值为 $min(b,a+c) \Rightarrow dist(A,C)$ 。
$$dist(A,C)=min(c+a, b)$$
4 转换
三角不等式的推广可得:对于某不等式 $x_i-x_j\leq a_k$,由 $x_j$ 向 $x_i$ 连一条长 $a_k$ 的有向边。
求 $x_i-x_j$ 的最大值即求 $x_j\rightarrow x_i$ 的最短路。
5 拓展
对于等式,将其转化为双不等式进行连边。
针对所考虑的问题,考虑不等式的形式。
由三角不等式的松弛原理:
若求 $x_i-x_j$ 的最大值,不等式应全部化为 $x_i-x_j\leq a_k$ 形式,求最短路。
若求 $x_i-x_j$ 的最小值,不等式应全部化为 $x_i-x_j\geq a_k$ 形式,求最长路。
6 它解(存在性)
若最短路上出现负权环,则 $x_a-x_b\leq T$,$T$ 趋近 $-inf$。
则 $x_a-x_b$ 不存在——无解。
若不连通,则 $x_a$ 与 $x_b$ 之间无约束——无限解。
7 矛盾推断
只需判断任意两点间是否存在 $x_a-x_b\leq T$ 无解即可。
若有解,则 $x_a-x_b\geq T$ 一定有解,因此只需判断一种不等式。
常见方法是全转“$\leq$”不等式形式,判断是否存在负环。
8 方程组求解
规定源点 $x_0=0$,定一个任意方程组如 $x_i-x_0\leq 0$ 进行约束,跑最短路求解,即可得到 $x_i$ 的任意一组解。
只需证明不存在对于两个求解的差值最大值,存在一种矛盾即可。
我们假设通过方程组求解而来有:$$x_1-x_0\leq A$$ $$x_2-x_0\leq B$$ $$x_2-x_1\leq C$$
则有 $$A=dist(x_0, x_1)$$ $$B=dist(x_0,x_2)$$ $$C=dist(x_1, x_2)$$
假设 $x_1-x_0=A, x_2-x_0=B$,若出现矛盾,情况为 $x_2-x_1=B-A>C$。
即 $C+A< B \Rightarrow dist(x_0, x_1)+dist(x_1, x_2)< dist(x_0, x_2)$,矛盾。
因此通过差分约束系统求解得来的差值最大值,若同时作为方程组的解,一定不会出现矛盾。